Playing with z3

It has not been very long since I got introduced to z3. But earlier I didn’t use it much. Now since I got to know the practicality of z3, I started using it. So out of my excitement and love for it, I started solving reverse challenges using z3.

This post is not gonna be a documentation or tutorial for z3, but rather a write-up of some reverse challenges which can be solved effortlessly with the use of z3.

This is gonna be post which contains write-ups of three challenges and it will go in the increasing level of difficulty in scripting.

Baby_reverse – Hack_Lu 2018

Challenge file : https://github.com/geethna/CTF-writeups/blob/master/chall

The challenge just had very few constraints. It just had a xor algorithm which xors the consecutive characters and checks the xor value with some data in memory.

The script is given below :

from z3 import *
mem_data=[0x0a, 0x0d, 0x06, 0x1c, 0x22, 0x38, 0x18, 0x26, 0x36, 0x0f, 0x39, 0x2b, 0x1c, 0x59, 0x42, 0x2c, 0x36, 0x1a, 0x2c, 0x26, 0x1c, 0x17, 0x2d, 0x39, 0x57, 0x43, 0x01, 0x07, 0x2b, 0x38, 0x09, 0x07, 0x1a, 0x01, 0x17, 0x13, 0x13, 0x17, 0x2d, 0x39, 0x0a, 0x0d, 0x06, 0x46, 0x5c, 0x7d, 0x00]
s=Solver()
a=[BitVec('a%d' %i,8) for i in range(46)]
for i in range(45):
    s.add(a[i]>=0x21)
    s.add(a[i]<=0x7d)
    s.add((a[i]^a[i+1])==mem_data[i])
while(s.check()==sat):
    m=s.model()
    w=''
    for i in range(46):
        w+=chr(m[a[i]].as_long())
    print w
    s.add(Or(a[0] != s.model()[a[0]],
             a[1] != s.model()[a[1]],
             a[2] != s.model()[a[2]],
             a[3] != s.model()[a[3]],
             a[4] != s.model()[a[4]],
             a[5] != s.model()[a[5]],
             a[6] != s.model()[a[6]],
             a[7] != s.model()[a[7]],
             a[8] != s.model()[a[8]],
             a[9] != s.model()[a[9]],
             a[10] != s.model()[a[10]],
             a[11] != s.model()[a[11]],
             a[12] != s.model()[a[12]],
             a[13] != s.model()[a[13]],
             a[14] != s.model()[a[14]],
             a[15] != s.model()[a[15]],
             a[16] != s.model()[a[16]],
             a[17] != s.model()[a[17]],
             a[18] != s.model()[a[18]],
             a[19] != s.model()[a[19]],
             a[20] != s.model()[a[20]],
             a[21] != s.model()[a[21]],
             a[22] != s.model()[a[22]],
             a[23] != s.model()[a[23]],
             a[24] != s.model()[a[24]],
             a[25] != s.model()[a[25]],
             a[26] != s.model()[a[26]],
             a[27] != s.model()[a[27]],
             a[28] != s.model()[a[28]],
             a[29] != s.model()[a[29]],
             a[30] != s.model()[a[30]],
             a[31] != s.model()[a[31]],
             a[32] != s.model()[a[32]],
             a[33] != s.model()[a[33]],
             a[34] != s.model()[a[34]],
             a[35] != s.model()[a[35]],
             a[36] != s.model()[a[36]],
             a[37] != s.model()[a[37]],
             a[38] != s.model()[a[38]],
             a[39] != s.model()[a[39]],
             a[40] != s.model()[a[40]],
             a[41] != s.model()[a[41]],
             a[42] != s.model()[a[42]],
             a[43] != s.model()[a[43]],
             a[44] != s.model()[a[44]]
))

Baby_first – Hackit 2018

Challenge link : https://github.com/geethna/CTF-writeups/blob/master/re1

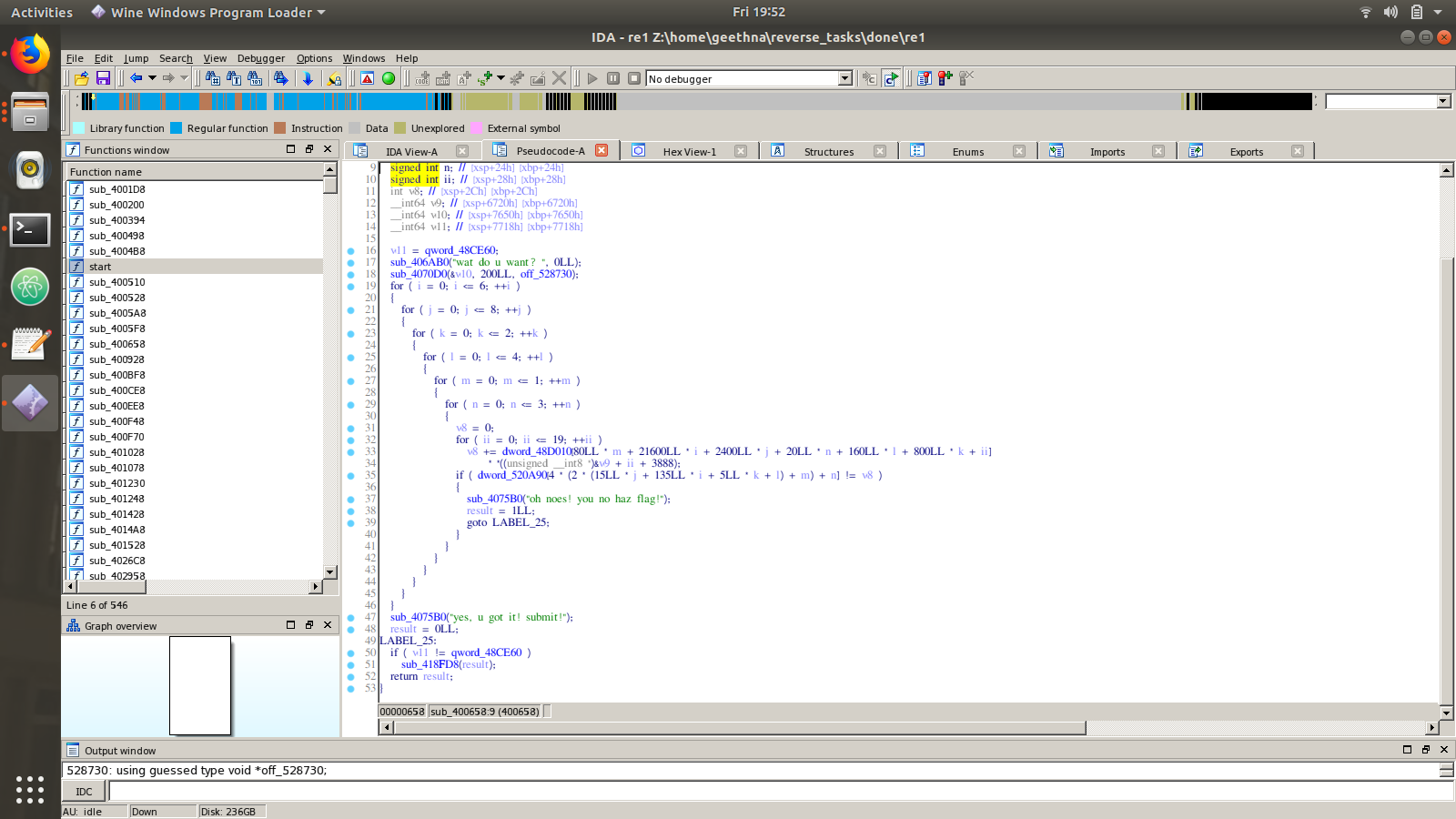
The challenge has 7 nested loops in it. From the innermost loop, we can understand that the string contains 20 characters. Also the check is a linear equation with 20 variables. To solve a linear equation of 20 variables, we need only 20 equations (Think in the matrix way). So what I did is generated 20 equations (So basically didn’t have to go through all the loops 😉 ). The pseudo-code generated in IDA looks something like this:

Below is the code I used to generated the correct flag:

from z3 import *
s=Solver()
a=[BitVec('a%d' %i,8) for i in range(20)]
s.add(62 * a[0] +23 * a[1] +49 * a[2] +47 * a[3] +63 * a[4] +36 * a[5] +91 * a[6] +6 * a[7] +31 * a[8] +16 * a[9] +11 * a[10] +91 * a[11] +2 * a[12] +49 * a[13] +73 * a[14] +19 * a[15] +77 * a[16] +76 * a[17] +67 * a[18] +86 * a[19] ==85050)
 
s.add(89 * a[0] +37 * a[1] +34 * a[2] +76 * a[3] +30 * a[4] +14 * a[5] +73 * a[6] +32 * a[7] +20 * a[8] +84 * a[9] +85 * a[10] +67 * a[11] +3 * a[12] +62 * a[13] +54 * a[14] +20 * a[15] +78 * a[16] +100 * a[17] +36 * a[18] +64 * a[19] ==91195)
 
s.add(100 * a[0] +71 * a[1] +39 * a[2] +26 * a[3] +74 * a[4] +73 * a[5] +83 * a[6] +95 * a[7] +62 * a[8] +90 * a[9] +8 * a[10] +11 * a[11] +77 * a[12] +32 * a[13] +19 * a[14] +9 * a[15] +23 * a[16] +76 * a[17] +62 * a[18] +88 * a[19] ==104053)
 
s.add(6 * a[0] +61 * a[1] +69 * a[2] +72 * a[3] +84 * a[4] +27 * a[5] +18 * a[6] +69 * a[7] +14 * a[8] +99 * a[9] +20 * a[10] +21 * a[11] +13 * a[12] +23 * a[13] +42 * a[14] +15 * a[15] +32 * a[16] +17 * a[17] +73 * a[18] +23 * a[19] ==74886)
 
s.add(20 * a[0] +74 * a[1] +49 * a[2] +43 * a[3] +63 * a[4] +96 * a[5] +4 * a[6] +88 * a[7] +84 * a[8] +95 * a[9] +36 * a[10] +51 * a[11] +89 * a[12] +39 * a[13] +2 * a[14] +41 * a[15] +77 * a[16] +11 * a[17] +22 * a[18] +20 * a[19] ==96859)
 
s.add(41 * a[0] +51 * a[1] +11 * a[2] +80 * a[3] +0 * a[4] +40 * a[5] +26 * a[6] +5 * a[7] +11 * a[8] +78 * a[9] +60 * a[10] +35 * a[11] +53 * a[12] +33 * a[13] +69 * a[14] +67 * a[15] +0 * a[16] +100 * a[17] +39 * a[18] +25 * a[19] ==78247)
 
s.add(28 * a[0] +27 * a[1] +3 * a[2] +57 * a[3] +64 * a[4] +23 * a[5] +68 * a[6] +49 * a[7] +26 * a[8] +16 * a[9] +20 * a[10] +66 * a[11] +58 * a[12] +3 * a[13] +51 * a[14] +28 * a[15] +39 * a[16] +5 * a[17] +56 * a[18] +52 * a[19] ==69704)
 
s.add(41 * a[0] +60 * a[1] +51 * a[2] +98 * a[3] +40 * a[4] +36 * a[5] +50 * a[6] +56 * a[7] +79 * a[8] +50 * a[9] +57 * a[10] +48 * a[11] +52 * a[12] +43 * a[13] +66 * a[14] +64 * a[15] +8 * a[16] +38 * a[17] +65 * a[18] +26 * a[19] ==93536)
 
s.add(65 * a[0] +88 * a[1] +53 * a[2] +36 * a[3] +29 * a[4] +84 * a[5] +21 * a[6] +98 * a[7] +92 * a[8] +14 * a[9] +94 * a[10] +29 * a[11] +42 * a[12] +83 * a[13] +45 * a[14] +34 * a[15] +44 * a[16] +78 * a[17] +44 * a[18] +77 * a[19] ==99410)
 
s.add(78 * a[0] +64 * a[1] +92 * a[2] +18 * a[3] +39 * a[4] +98 * a[5] +46 * a[6] +7 * a[7] +60 * a[8] +48 * a[9] +31 * a[10] +74 * a[11] +40 * a[12] +26 * a[13] +70 * a[14] +29 * a[15] +23 * a[16] +13 * a[17] +100 * a[18] +33 * a[19] ==91294)
 
s.add(38 * a[0] +63 * a[1] +66 * a[2] +53 * a[3] +7 * a[4] +87 * a[5] +70 * a[6] +77 * a[7] +51 * a[8] +98 * a[9] +100 * a[10] +83 * a[11] +75 * a[12] +67 * a[13] +7 * a[14] +41 * a[15] +63 * a[16] +80 * a[17] +45 * a[18] +93 * a[19] ==109711)
 
s.add(18 * a[0] +68 * a[1] +76 * a[2] +85 * a[3] +6 * a[4] +36 * a[5] +24 * a[6] +52 * a[7] +57 * a[8] +0 * a[9] +4 * a[10] +95 * a[11] +88 * a[12] +72 * a[13] +46 * a[14] +9 * a[15] +84 * a[16] +31 * a[17] +22 * a[18] +94 * a[19] ==85114)
 
s.add(99 * a[0] +58 * a[1] +9 * a[2] +72 * a[3] +28 * a[4] +95 * a[5] +11 * a[6] +74 * a[7] +2 * a[8] +46 * a[9] +45 * a[10] +62 * a[11] +10 * a[12] +19 * a[13] +97 * a[14] +30 * a[15] +91 * a[16] +73 * a[17] +83 * a[18] +55 * a[19] ==104598)
 
s.add(100 * a[0] +33 * a[1] +92 * a[2] +7 * a[3] +60 * a[4] +75 * a[5] +30 * a[6] +85 * a[7] +62 * a[8] +100 * a[9] +47 * a[10] +89 * a[11] +14 * a[12] +47 * a[13] +73 * a[14] +79 * a[15] +92 * a[16] +99 * a[17] +52 * a[18] +27 * a[19] ==118115)
 
s.add(25 * a[0] +19 * a[1] +3 * a[2] +89 * a[3] +29 * a[4] +2 * a[5] +14 * a[6] +29 * a[7] +42 * a[8] +23 * a[9] +88 * a[10] +95 * a[11] +76 * a[12] +54 * a[13] +1 * a[14] +47 * a[15] +77 * a[16] +50 * a[17] +50 * a[18] +23 * a[19] ==76597)
 
s.add(100 * a[0] +69 * a[1] +71 * a[2] +97 * a[3] +72 * a[4] +34 * a[5] +41 * a[6] +8 * a[7] +35 * a[8] +40 * a[9] +91 * a[10] +49 * a[11] +54 * a[12] +8 * a[13] +20 * a[14] +2 * a[15] +15 * a[16] +73 * a[17] +77 * a[18] +84 * a[19] ==91860)
 
s.add(46 * a[0] +81 * a[1] +51 * a[2] +9 * a[3] +98 * a[4] +99 * a[5] +47 * a[6] +61 * a[7] +38 * a[8] +97 * a[9] +60 * a[10] +88 * a[11] +63 * a[12] +54 * a[13] +30 * a[14] +15 * a[15] +57 * a[16] +72 * a[17] +60 * a[18] +44 * a[19] ==108325)
 
s.add(32 * a[0] +42 * a[1] +30 * a[2] +20 * a[3] +56 * a[4] +4 * a[5] +35 * a[6] +73 * a[7] +13 * a[8] +42 * a[9] +64 * a[10] +90 * a[11] +81 * a[12] +31 * a[13] +82 * a[14] +43 * a[15] +91 * a[16] +93 * a[17] +4 * a[18] +1 * a[19] ==86408)
 
s.add(55 * a[0] +32 * a[1] +51 * a[2] +3 * a[3] +32 * a[4] +59 * a[5] +84 * a[6] +20 * a[7] +96 * a[8] +7 * a[9] +99 * a[10] +38 * a[11] +3 * a[12] +21 * a[13] +80 * a[14] +88 * a[15] +50 * a[16] +46 * a[17] +34 * a[18] +68 * a[19] ==79996)
 
s.add(70 * a[0] +30 * a[1] +76 * a[2] +29 * a[3] +33 * a[4] +50 * a[5] +95 * a[6] +47 * a[7] +11 * a[8] +4 * a[9] +96 * a[10] +82 * a[11] +91 * a[12] +52 * a[13] +68 * a[14] +83 * a[15] +28 * a[16] +27 * a[17] +89 * a[18] +30 * a[19] ==92996)
print s.check()
while(s.check()==sat):
m=s.model()
w=''
for i in range(20):
w+=chr(m[a[i]].as_long())
print w
s.add(Or(a[0] != s.model()[a[0]],
a[1] != s.model()[a[1]],
a[2] != s.model()[a[2]],
a[3] != s.model()[a[3]],
a[4] != s.model()[a[4]],
a[5] != s.model()[a[5]],
a[6] != s.model()[a[6]],
a[7] != s.model()[a[7]],
a[8] != s.model()[a[8]],
a[9] != s.model()[a[9]],
a[10] != s.model()[a[10]],
a[11] != s.model()[a[11]],
a[12] != s.model()[a[12]],
a[13] != s.model()[a[13]],
a[14] != s.model()[a[14]],
a[15] != s.model()[a[15]],
a[16] != s.model()[a[16]],
a[17] != s.model()[a[17]],
a[18] != s.model()[a[18]],
a[19] != s.model()[a[19]]))

Quadmath – Hackim18

Challenge file : https://github.com/geethna/CTF-writeups/blob/master/quadmath.stripped

This challenge was completely scripting. There was nothing much to reverse. All the constraints were given in the challenge itself. There were 65 functions. Each function has an equation which involves alternate characters of the flag. The constraints were a little less I guess, because the challenge accepted many flags. Below is the code :

'''for i in range(20,66):
print "s.add(Or(a["+str(i)+"]*a["+str(i)+"]-203*a["+str(i)+"]==-10296),(a["+str(i+2)+"]*a["+str(i+2)+"]-203*a["+str(i+2)+"]==-10296))"
#print " a["+str(i)+"] != s.model()[a["+str(i)+"]],"
 
'''# The above python code I used for generating the constraints.
 
from z3 import *
a=[BitVec('a%d' %i,8) for i in range(68)]
s=Solver()
s.add(And(a[0]*a[0]-203*a[0]==-10296),(a[2]*a[2]-203*a[2]==-10296))
s.add(And(a[1]*a[1]-204*a[1]==-10379),(a[3]*a[3]-204*a[3]==-10379))
s.add(And(a[2]*a[2]-204*a[2]==-10395),(a[4]*a[4]-204*a[4]==-10395))
s.add(And(a[3]*a[3]-216*a[3]==-11663),(a[5]*a[5]-216*a[5]==-11663))
s.add(And(a[4]*a[4]-154*a[4]==-5145),(a[6]*a[6]-154*a[6]==-5145))
s.add(And(a[5]*a[5]-165*a[5]==-6104),(a[7]*a[7]-165*a[7]==-6104))
s.add(And(a[6]*a[6]-172*a[6]==-6027),(a[8]*a[8]-172*a[8]==-6027))
s.add(And(a[7]*a[7]-95*a[7]==-2184),(a[9]*a[9]-95*a[9]==-2184))
s.add(And(a[8]*a[8]-210*a[8]==-10701),(a[10]*a[10]-210*a[10]==-10701))
s.add(And(a[9]*a[9]-87*a[9]==-1872),(a[11]*a[11]-87*a[11]==-1872))
s.add(And(a[10]*a[10]-174*a[10]==-7569),(a[12]*a[12]-174*a[12]==-7569))
s.add(And(a[11]*a[11]-143*a[11]==-4560),(a[13]*a[13]-143*a[13]==-4560))
s.add(And(a[12]*a[12]-206*a[12]==-10353),(a[14]*a[14]-206*a[14]==-10353))
s.add(And(a[13]*a[13]-206*a[13]==-10545),(a[15]*a[15]-206*a[15]==-10545))
s.add(And(a[14]*a[14]-238*a[14]==-14161),(a[16]*a[16]-238*a[16]==-14161))
s.add(And(a[15]*a[15]-206*a[15]==-10545),(a[17]*a[17]-206*a[17]==-10545))
s.add(And(a[16]*a[16]-238*a[16]==-14161),(a[18]*a[18]-238*a[18]==-14161))
s.add(And(a[17]*a[17]-143*a[17]==-4560),(a[19]*a[19]-143*a[19]==-4560))
s.add(And(a[18]*a[18]-238*a[18]==-14161),(a[20]*a[20]-238*a[20]==-14161))
s.add(And(a[19]*a[19]-143*a[19]==-4560),(a[21]*a[21]-143*a[21]==-4560))
s.add(And(a[20]*a[20]-206*a[20]==-10353),(a[22]*a[22]-206*a[22]==-10353))
s.add(And(a[21]*a[21]-206*a[21]==-10545),(a[23]*a[23]-206*a[23]==-10545))
s.add(And(a[22]*a[22]-174*a[22]==-7569),(a[24]*a[24]-174*a[24]==-7569))
s.add(And(a[23]*a[23]-206*a[23]==-10545),(a[25]*a[25]-206*a[25]==-10545))
s.add(And(a[24]*a[24]-208*a[24]==-10527),(a[26]*a[26]-208*a[26]==-10527))
s.add(And(a[25]*a[25]-143*a[25]==-4560),(a[27]*a[27]-143*a[27]==-4560))
s.add(And(a[26]*a[26]-238*a[26]==-14157),(a[28]*a[28]-238*a[28]==-14157))
s.add(And(a[27]*a[27]-143*a[27]==-4560),(a[29]*a[29]-143*a[29]==-4560))
s.add(And(a[28]*a[28]-221*a[28]==-12168),(a[30]*a[30]-221*a[30]==-12168))
s.add(And(a[29]*a[29]-147*a[29]==-4940),(a[31]*a[31]-147*a[31]==-4940))
s.add(And(a[30]*a[30]-222*a[30]==-12272),(a[32]*a[32]-222*a[32]==-12272))
s.add(And(a[31]*a[31]-103*a[31]==-2652),(a[33]*a[33]-103*a[33]==-2652))
s.add(And(a[32]*a[32]-213*a[32]==-11210),(a[34]*a[34]-213*a[34]==-11210))
s.add(And(a[33]*a[33]-160*a[33]==-5559),(a[35]*a[35]-160*a[35]==-5559))
s.add(And(a[34]*a[34]-147*a[34]==-4940),(a[36]*a[36]-147*a[36]==-4940))
s.add(And(a[35]*a[35]-225*a[35]==-12644),(a[37]*a[37]-225*a[37]==-12644))
s.add(And(a[36]*a[36]-156*a[36]==-5408),(a[38]*a[38]-156*a[38]==-5408))
s.add(And(a[37]*a[37]-211*a[37]==-11020),(a[39]*a[39]-211*a[39]==-11020))
s.add(And(a[38]*a[38]-219*a[38]==-11960),(a[40]*a[40]-219*a[40]==-11960))
s.add(And(a[39]*a[39]-202*a[39]==-10165),(a[41]*a[41]-202*a[41]==-10165))
s.add(And(a[40]*a[40]-164*a[40]==-5635),(a[42]*a[42]-164*a[42]==-5635))
s.add(And(a[41]*a[41]-215*a[41]==-11556),(a[43]*a[43]-215*a[43]==-11556))
s.add(And(a[42]*a[42]-157*a[42]==-5292),(a[44]*a[44]-157*a[44]==-5292))
s.add(And(a[43]*a[43]-161*a[43]==-5724),(a[45]*a[45]-161*a[45]==-5724))
s.add(And(a[44]*a[44]-203*a[44]==-10260),(a[46]*a[46]-203*a[46]==-10260))
s.add(And(a[45]*a[45]-140*a[45]==-4611),(a[47]*a[47]-140*a[47]==-4611))
s.add(And(a[46]*a[46]-143*a[46]==-4560),(a[48]*a[48]-143*a[48]==-4560))
s.add(And(a[47]*a[47]-198*a[47]==-9657),(a[49]*a[49]-198*a[49]==-9657))
s.add(And(a[48]*a[48]-135*a[48]==-4176),(a[50]*a[50]-135*a[50]==-4176))
s.add(And(a[49]*a[49]-206*a[49]==-10545),(a[51]*a[51]-206*a[51]==-10545))
s.add(And(a[50]*a[50]-206*a[50]==-10353),(a[52]*a[52]-206*a[52]==-10353))
s.add(And(a[51]*a[51]-143*a[51]==-4560),(a[53]*a[53]-143*a[53]==-4560))
s.add(And(a[52]*a[52]-230*a[52]==-13209),(a[54]*a[54]-230*a[54]==-13209))
s.add(And(a[53]*a[53]-167*a[53]==-5712),(a[55]*a[55]-167*a[55]==-5712))
s.add(And(a[54]*a[54]-206*a[54]==-10545),(a[56]*a[56]-206*a[56]==-10545))
s.add(And(a[55]*a[55]-238*a[55]==-14161),(a[57]*a[57]-238*a[57]==-14161))
s.add(And(a[56]*a[56]-206*a[56]==-10545),(a[58]*a[58]-206*a[58]==-10545))
s.add(And(a[57]*a[57]-167*a[57]==-5712),(a[59]*a[59]-167*a[59]==-5712))
s.add(And(a[58]*a[58]-230*a[58]==-13209),(a[60]*a[60]-230*a[60]==-13209))
s.add(And(a[59]*a[59]-143*a[59]==-4560),(a[61]*a[61]-143*a[61]==-4560))
s.add(And(a[60]*a[60]-206*a[60]==-10353),(a[62]*a[62]-206*a[62]==-10353))
s.add(And(a[61]*a[61]-206*a[61]==-10545),(a[63]*a[63]-206*a[63]==-10545))
s.add(And(a[62]*a[62]-135*a[62]==-4176),(a[64]*a[64]-135*a[64]==-4176))
s.add(And(a[63]*a[63]-198*a[63]==-9657),(a[65]*a[65]-198*a[65]==-9657))
s.add(And(a[64]*a[64]-87*a[64]==-1872),(a[66]*a[66]-87*a[66]==-1872))
s.add(And(a[65]*a[65]-212*a[65]==-10875),(a[66]*a[67]-212*a[67]==-10875))
s.add(a[0]==104)
s.add(a[1]==97)
s.add(a[2]==99)
s.add(a[3]==107)
s.add(a[4]==105)
s.add(a[5]==109)
s.add(a[6]==49)
s.add(a[7]==56)
s.add(a[8]==123)
s.add(a[9]==39)
s.add(a[66]==39)
for i in range(0,67):
s.add(And(a[i]>=33),(a[i]= 21)
print s.check()
while(s.check()==sat):
m=s.model()
w=''
for i in range(67):
w+=chr(m[a[i]].as_long())
print w
s.add(Or(a[0] != s.model()[a[0]],
a[1] != s.model()[a[1]],
a[2] != s.model()[a[2]],
a[3] != s.model()[a[3]],
a[4] != s.model()[a[4]],
a[5] != s.model()[a[5]],
a[6] != s.model()[a[6]],
a[7] != s.model()[a[7]],
a[8] != s.model()[a[8]],
a[9] != s.model()[a[9]],
a[10] != s.model()[a[10]],
a[11] != s.model()[a[11]],
a[12] != s.model()[a[12]],
a[13] != s.model()[a[13]],
a[14] != s.model()[a[14]],
a[15] != s.model()[a[15]],
a[16] != s.model()[a[16]],
a[17] != s.model()[a[17]],
a[18] != s.model()[a[18]],
a[19] != s.model()[a[19]],
a[20] != s.model()[a[20]],
a[20] != s.model()[a[20]],
a[21] != s.model()[a[21]],
a[22] != s.model()[a[22]],
a[23] != s.model()[a[23]],
a[24] != s.model()[a[24]],
a[25] != s.model()[a[25]],
a[26] != s.model()[a[26]],
a[27] != s.model()[a[27]],
a[28] != s.model()[a[28]],
a[29] != s.model()[a[29]],
a[30] != s.model()[a[30]],
a[31] != s.model()[a[31]],
a[32] != s.model()[a[32]],
a[33] != s.model()[a[33]],
a[34] != s.model()[a[34]],
a[35] != s.model()[a[35]],
a[36] != s.model()[a[36]],
a[37] != s.model()[a[37]],
a[38] != s.model()[a[38]],
a[39] != s.model()[a[39]],
a[40] != s.model()[a[40]],
a[41] != s.model()[a[41]],
a[42] != s.model()[a[42]],
a[43] != s.model()[a[43]],
a[44] != s.model()[a[44]],
a[45] != s.model()[a[45]],
a[46] != s.model()[a[46]],
a[47] != s.model()[a[47]],
a[48] != s.model()[a[48]],
a[49] != s.model()[a[49]],
a[50] != s.model()[a[50]],
a[51] != s.model()[a[51]],
a[52] != s.model()[a[52]],
a[53] != s.model()[a[53]],
a[54] != s.model()[a[54]],
a[55] != s.model()[a[55]],
a[56] != s.model()[a[56]],
a[57] != s.model()[a[57]],
a[58] != s.model()[a[58]],
a[59] != s.model()[a[59]],
a[60] != s.model()[a[60]],
a[61] != s.model()[a[61]],
a[62] != s.model()[a[62]],
a[63] != s.model()[a[63]],
a[64] != s.model()[a[64]],
a[65] != s.model()[a[65]],
a[66] !=s.model()[a[66]],
))

So that was it. I think z3 is really cool. I recommend everybody to try it out.

I didn’t actually explain the reversing process in any of the challenge discussed because the context was different. But if you really want to know about it, let me know in the comments 🙂 .

Thank you!